الأعداد الأولية من 1 إلى 1000

تعرف الأعداد الأولية على أنها أعداد صحيحة موجبة أكبر من واحد قابلة للقسمة على رقمين فقط الرقم نفسه والرقم الذي لا يترك باقيًا؛ على سبيل المثال الأرقام 13 و 17 و 28.

فإن الأعداد غير الأولية أو الأعداد المركبة هي أعداد صحيحة موجبة أكبر من العدد الذي يقبل القسمة على رقم آخر غير نفسها وليس هي نفسها.

على سبيل المثال الرقم (28) الذي له عدة عوامل، فضع في اعتبارك حقيقة أن العددين 0 و 1 مستبعدان دائمًا من قائمة الأرقام الأولية والمركبة بينما يعتبر الرقم 2 أصغر الأعداد الأولية.

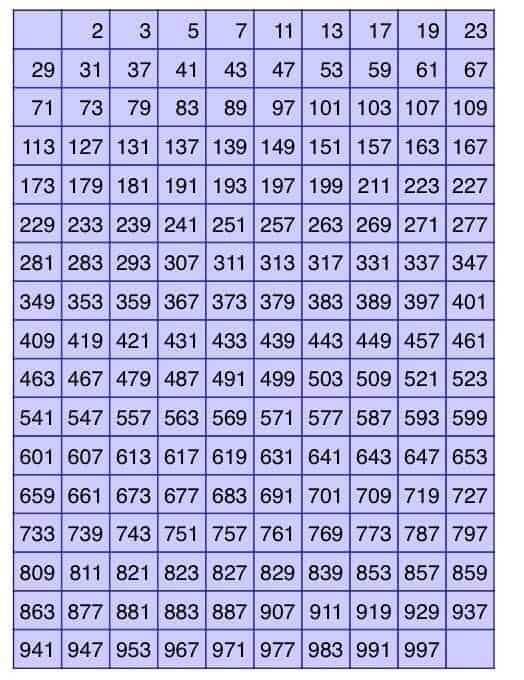
جدول الأعداد الأولية من 1 إلى 1000

تعريف

• العدد الأولي هو عدد صحيح موجب ويمكننا أن نرى أنه يجب أن يكون أكبر من العدد الصحيح.
• فيمكننا أن نرى أيضًا أن هذا الرقم لا يقبل القسمة على أكثر من رقمين وأن العددين يكونان نفس العدد عندما نقسمه.
• فهذا صحيح لكل من الرقم نفسه وحقيقة أنه غير قابل للقسمة.
• فمن مزايا العدد الأولي أنه ليس له نهاية.
• ومن هنا نكتشف فرقًا بينه وبين العدد غير الأولي وهو أنه مجزأ.

ما هي أهمية الأعداد الأولية

نكتشف أن هذه الأعداد تحظى بتقدير كبير من قبل العلماء في مجموعة متنوعة من المجالات؛ فنكتشف أيضًا أن الأعداد الأولية لم يتم إهمالها حتى هذه النقطة.

• حيث نكتشف أن قدماء المصريين كانوا أول من أبدوا اهتمامًا بهذه الأرقام.
• وقد كشفت الدراسات أن الإغريق أجروا أيضًا أبحاثًا مستفيضة في هذه الأرقام مما دفعنا للاعتقاد بأن العالم الشهير إقليدس كان أول من اكتشف أن العدد الأولي ليس له نهاية. 
• فكان هذا هو الحال منذ العصور القديمة، ونتيجة لذلك يمكننا أن نستنتج أن دراسة الأعداد الأولية كانت مهمة للغاية حتى في أقدم العصور.
• لذلك من أجل فهم أهمية هذه الأرقام.

1. يجب أولًا الانتباه إليها في الماضي.
2. وتحقيق النجاح فيها حتى نتمكن بعد ذلك من دراسة الأعداد المركبة من أجل الحصول على فهم شامل لها. 

• لذلك هناك حقيقة أخرى مثيرة للاهتمام حول هذه الأرقام هي أن هناك واحدًا منها أثار قدرًا كبيرًا من الجدل حول ما إذا كان عددًا أوليًا أم لا.

1. في هذه الحالة نرى أن للعدد مقامًا واحدًا وهو واحد.
2. ولكن يجب تقسيم العدد الأولي إلى رقمين أحدهما هو نفس الرقم الآخر.
3. ونكتشف أن أحد الأرقام لا يمثل عدد أولي لذلك نجد تكرارًا للرقم مع الرقم واحد وهو ما لا ينبغي أن يكون عليه الحال.

اقرأ أيضًا: بحث عن منصة احسان الوطنية للعمل الخيري

كيف تعرف الأرقام الأولية

يمكن اكتشاف الأعداد الأولية بإحدى طريقتين:

التحليل إلى العوامل: 

يمكن لعلماء الرياضيات تحديد ما إذا كان الرقم أوليًا أم لا باستخدام هذه العملية ومن أجل استخدام طريقة التحليل، يجب أن تفهم أن العامل هو أي رقم يمكن ضربه في رقم آخر للحصول على نفس النتيجة مثل:

• الأصل رقم، حيث تتضمن الأمثلة العوامل الأولية للرقم 10 الذي يمثل الرقمين 2 و 5؛ لأنه عندما يتم ضرب هذه الأعداد الصحيحة معًا ستكون النتيجة 10.
• والعدد 1 و 10 من عوامل العدد 10 لأنه عندما يتم ضرب أحدهما في الآخر ستكون النتيجة 10.
• ومع ذلك فإن العوامل الأولية للعدد 10 هي فقط العددين 2 و 5 لأن العددين واحد وعشرة ليسا أعدادًا أولية.

اقرأ أيضًا: بحث عن كوكب الأرض معلومات تفصيلية

الاستفادة من الآلة الحاسبة:

لتحديد ما إذا كان الرقم أوليًا أم لا يمكن استخدام الآلات الحاسبة ومفهوم القسمة جنبًا إلى جنب، على سبيل المثال:

• لتحديد ما إذا كان الرقم 57 عددًا أوليًا، نقسمه أولًا على الرقم 2.
• واكتشفنا أن حاصل القسمة هو 27.5، وهو ليس عددًا صحيحًا.
• ثم نقسم الرقم 57 على 3، والنتيجة هي 19 (وهو ليس عددًا صحيحًا).
• فنظرًا لكونه عددًا صحيحًا فإن كلا من 19 و 3 عاملان للعدد 57 مما يشير إلى أنه ليس عددًا أوليًا. 

ختامًا لقد غطينا كل ما يتعلق بأهمية الأعداد الأولية في المقال بالإضافة إلى تعريف وشرح بعض الأمثلة لها، كما أوضحنا أيضًا كيفية تحديد عدد أولي من عدد مركب بالإضافة إلى ما هي أهمية وخصائص الأرقام الأولية.